
If two linear equations are given the same slope it means that they are parallel and if the product of two slopes m1*m2=-1 the two linear equations are said to be perpendicular. The slope of a line passing through points (x1,y1) and (x2,y2) is given by The slope, m, is here 1 and our b (y-intercept) is 7. If m, the slope, is negative the functions value decreases with an increasing x and the opposite if we have a positive slope.Īn equation such as y=x+7 is linear and there are an infinite number of ordered pairs of x and y that satisfy the equation. This form is called the slope-intercept form.

f(2) means that we should find the value of our function when x equals 2.Ī function is linear if it can be defined byī is the value of the function when x equals zero or the y-coordinate of the point where the line crosses the y-axis in the coordinate plane.
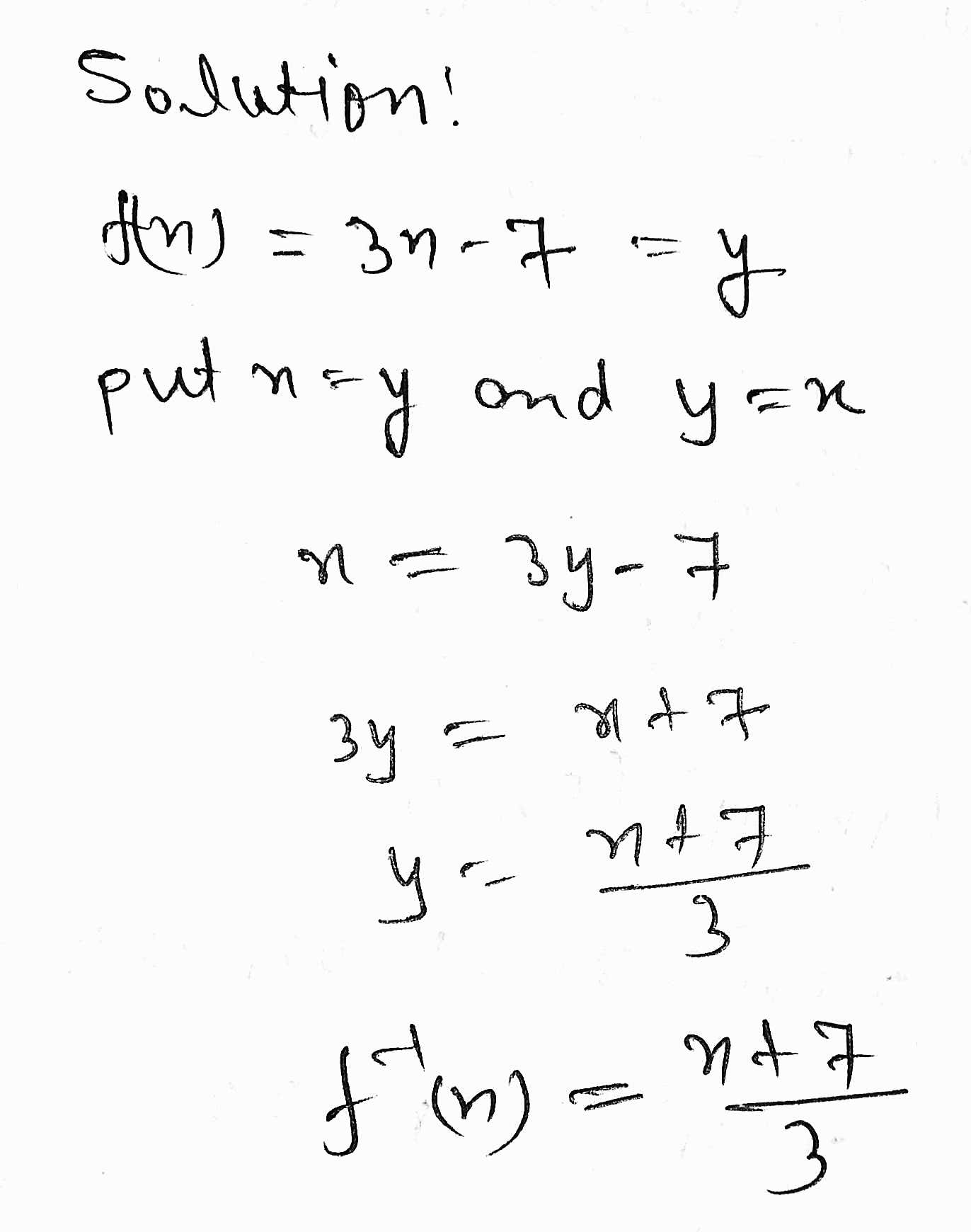
It is common to name a function either f(x) or g(x) instead of y. A function assigns exactly one output to each input of a specified type. In our example above, x is the independent variable and y is the dependent variable.Ī function is an equation that has only one answer for y for every x. Since 8 8 is a true statement, 2 is the solution of the equation. To check, replace the x in the original equation with the solution. To do so, we divide both sides of the equation by -4 and then simplify. The variable which we assign the value we call the independent variable, and the other variable is the dependent variable, since it value depends on the independent variable. To solve the equation for x, we need to rewrite the equation in the form x number. In our equation y=x+7, we have two variables, x and y. We could instead have assigned a value for y and solved the equation to find the matching value of x.

If we would have assigned a different value for x, the equation would have given us another value for y. Interactive algebra calculators for solving equations, polynomials, rational functions, simplification, vectors, matrices, linear algebra, quaternions. This is the default behaviour, if it's an inconvenience and your calculation does not need exact arithmetic then the notation of powers of ten can be recovered everywhere wrapping the definition of splfy in N.If we in the following equation y=x+7 assigns a value to x, the equation will give us a value for y. Note that approximate numbers get printed using the scientific notation while exact numbers will be expanded at output: splfy/(1 10^2)] It stays within exact arithmetic where all numbers are exact: splfy/(1 10^22)]Īnd converts a relevant part of the output to approximate numbers when a part of the input is: splfy/(1 10^22)] This also works in the other examples provided. (* Precision is retained, as seen in InputForm: Sqrt *)

In the latter case others have already provided the best approaches but if it's simply that the numbers are large, with no particular bound to decimal base, then probably the best you can do is force Mathematica to merge the prefactor into the square root simply like this: splfy := Sqrt] x + y 21 equation 1 x - y 9 equation 2 Rearrange equation 2 to make equation 3 (Equation 3 is just to sub into the other eqs) x 9 + y equation 3 Sub equation 3 into 1 (9 + y) + y 21 9 + 2y 21 2y. Solve: Let x be a number, and Let y be another number. In this case the scenario is quite different than in the original formulation of the question which would suggest that the numbers involved are still very simple in decimal base. This question requires 2 equation to solve thus it is call simultaneous equation. Rationalize does not give a substantial simplification. A closer example to my application is this: 1.*10^-22 Sqrt.


 0 kommentar(er)
0 kommentar(er)
